Introduction

This paper is intended for game developers who are interested in a new approach to developing an environment engine. An algorithm is presented for quickly determining the visible portion of an environment given a view point and a view frustum. A very similar algorithm can be used for detecting collisions with the environment. The algorithm has the advantages of a short computation time during level building, dynamically computing the visibility set to accommodate changing environments, and not placing limitations on the environment creation process. Its disadvantages are discussed at the end of the paper.

This algorithm is currently being used in Bungie's upcoming third person action game, Oni. Its advantages allow the architects who created Oni's environments to focus on creating great environments without having to worry about limiting the visibility or defining the visibility via portals. The algorithm easily allows for standard off the shelf authoring tools to be used in place of custom-built tools.

Definition of Problem

Here an environment is defined as a collection of geometric primitives, usually polygons, that as a whole define the shape and look of the world in a video game. These primitives are treated as static in that they do not move any significant amount. Higher level primitives, such as curved surfaces, can be used by subdivision into simpler primitives.

The act of determining the visible portion of an environment can be called hidden surface complexity reduction. This means taking a large set of surfaces (polygons) and culling them into a much smaller set of surfaces that are rendered to the display device. This process is usually accomplished by putting all the static primitives of an environment into some data structure based on spatial division. An algorithm is then used to extract the primitives from this data structure.

Another term for this process is visible surface determination. The term hidden surface complexity reduction was chosen because the algorithm does not try to find the optimal set of visible surfaces. Instead it tries to reduce the visible surface complexity enough to allow real-time rendering on 3D hardware.

Traditional Approaches

One of the most common spatial subdivision data structures is the binary space partitioning (BSP) tree, which has been documented and discussed at length [1]. The basic idea of a BSP tree is that space is subdivided into two regions based on a plane. The tree is constructed by picking a splitting plane from the set of primitives in the environment and dividing the rest of the primitives based on which side of the plane they lie. The process is repeated recursively for each side until no more primitives remain.

To keep the size of the BSP tree reasonable, a mechanism called a portal is usually introduced for large primitive sets such as environments. A portal limits visibility between different parts of the environment that have mutually exclusive primitive visibility sets. For example, a door that separates two rooms is a portal. Typically, the portals in an environment are authored by hand but can also be pre-computed to some extent. The set of visible primitives at each BSP leaf node is pre-computed to save the run-time cost of determining the visible primitive set.

Introduction to Oct Trees

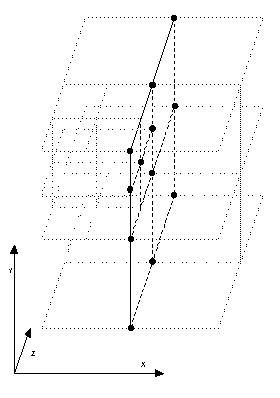
Here a data structure and an algorithm based on an oct tree are presented. While a BSP tree partitions space into two sub-spaces based on planes, an oct tree subdivides space into eight axis-aligned sub-spaces called octants. At the root of an oct tree is a rectangular volume that encloses the entire environment. Subdividing each of the x, y, and z planes into eight octants forms the eight children of a node. A leaf node has no children and meets the condition of either enclosing a small enough volume or a small enough set of primitives. An interior node is an octant with eight children that may or may not be leaf nodes.

A diagram of how an octant is subdivided into eight children is shown in Figure 1.

Figure 1
 
 

Oct Tree Data Structure

One method for storing an oct tree is presented here. Obviously, there are many ways to represent an oct tree structure in memory. However, this method has several advantages: It is compact for good cache locality and its octant size is always a power of two, which gives it an exact representation as a 32-bit floating point number. This prevents precision errors when determining which primitives are contained by an octant. Each octant is always a cube so that only one dimension needs to be stored.

Additionally, leaf node adjacency information is stored. Each leaf node contains a pointer to its adjacent octant for each of the six sides of the octant. In the case that an adjacent octant is an interior node and not a leaf node, a pointer to a quad tree is kept. A quad tree is used because all the possible leaf nodes that are adjacent to a larger octant form a quad tree. The leaf nodes of the quad tree are simply the leaf octant nodes. Figure 2 shows Figure 1 subdivided one additional level in the front, top, left octant. Note how the nodes form a quad tree on the YZ plane.

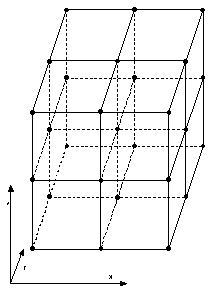Figure 2

Each octant must also store all the primitives that intersect it. It is assumed that all the primitives are stored in a linear list. A large linear array of indices is used to index into the primitive list. Each leaf octant stores an initial offset into this array of indices and a length of how many primitives are contained within the octant. This is stored in primitive_indirect_index_encode and is encoded as a 24-bit offset and an 8-bit length. This means that a leaf node can hold a maximum of 256 primitives. A diagram is shown in Figure 3.

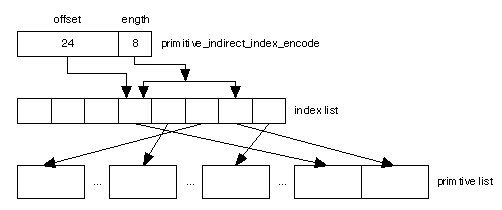Figure 3

Note that the same primitive is contained in as many leaf nodes as it intersects. Additionally, there is no need to subdivide primitives across leaf node boundaries.

Each leaf node contains information about its size and absolute position in the tree. The algorithms presented below will use this information. The field dimension_encode contains this information. It is encoded into a 32-bit unsigned integer for compactness. The first 5 bits encode the leaf node size. The next three 9-bit fields encode the maximum x, y, and z positions of the node in the tree. The minimum x, y, and z values are computed by subtracting the node size from the maximum x, y, and z values.

How these bit fields are converted into real floating point numbers is based on the size of the environment. Since 9 bits are used to encode the possible positions of a leaf node, the smallest leaf node is the maximum dimension of the environment divided by 512. Likewise, the largest dimension for a leaf node will be 32 times the smallest dimension. For example, let's say a unit is 1 foot and the largest possible environment can be 8,192 feet. This means that the smallest leaf node will be 16 feet and the largest will be 512 feet. As long as the environment contains less than 256 primitives with a 16x16x16 foot volume, this structure will work fine. An environment with a greater density will have to have a smaller maximum dimension.

In practice this did not prove restrictive in the Oni project despite the game's very dense polygonal areas such as staircases with hand railings. The largest environment was over 40,000 polygons and spanned approximately a half-mile. There will no doubt be games that require more resources than this in the future and the oct tree data structure can be modified to store 16 bits for each of the x, y, z, and octant width fields. Of course, this will mean an additional 4 bytes of storage for each octant.

    The code for this data structure is listed in Appendix A.

Algorithm for Fast Ray Casting

The core algorithm used for both hidden surface complexity reduction and collision detection is casting a ray and tracing all the leaf octants that contain the ray. It is important that the octants are traversed in order starting from the origin of the ray and then proceeding along the path of the ray.

The basic idea is that we first determine the leaf octant that contains the starting point of the ray. Then based on the ray vector we find the next adjacent leaf octant along the ray. This process is repeated until the entire ray has been traversed or some other termination criterion has been met.

The most challenging part of this algorithm is determining the next adjacent leaf octant. The first step is to determine which side of the octant the ray exits. The approach is to use elimination to remove the 5 sides that it does not exit, thus leaving the correct side as the only choice.

The six sides of an octant are each given a name as follows: Xpos, Xneg, Ypos, Yneg, Zpos, and Zneg. This naming scheme follows the convention of naming the side after the axis its plane crosses and designating it positive if its X component is greater then the X component of the opposite side. Figure 4 shows a two-dimensional example.

The first 3 rejections are trivial. The sign of the ray vector's X, Y, and Z components is examined. If the component is positive, then we can eliminate the negative side. If the component is negative, then the positive side is removed. For example, if the X component is ?0.3, the ray is traveling in the negative X direction, so it can't possibly exit the cube on the positive X side, therefore the positive X side is eliminated.

Unfortunately, removing the final 2 sides is more difficult. Essentially, the slope of the ray projected onto a 2D plane must be examined to determine which of the remaining sides can be rejected. It is easiest to first consider the two-dimensional quad tree case. Now the problem is to move from one quadrant to the next.

Let's take an example shown in Figure 4.

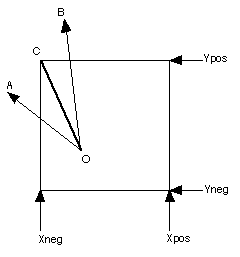Figure 4

For both rays OA and OB, we can eliminate the Xpos and Yneg side from the direction of each ray. The problem is to eliminate the final side. The solution is to compare the slope of the ray with the slope of the line segment from point O to point C. If the slope of the ray is greater than the slope of OC, the Ypos side is chosen. Otherwise, the Xneg side is chosen. This can be generalized in that if the slope of the ray is greater than the slope of OC, pick the Y-axis, otherwise pick the X-axis. This makes sense intuitively, if the ray is rising faster than OC, it will cross the Y-axis first.

The equation is as follows:

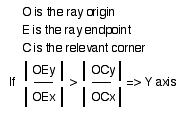
This can be simplified to avoid the division:

Note that this is essentially the Bresenham algorithm.

To solve the three-dimensional case we simply apply the above technique twice. We first project onto the XY plane to eliminate one side. Second, if we eliminated X, then we project onto the YZ plane, otherwise we eliminated Y so we then project onto XZ. This yields the final result. Since we previously determined whether we were crossing the positive or negative side of the axis, we are finished.

Now that we know which side of the octant we are crossing, there is one more potential complication. If the side that we are crossing is adjacent to a leaf node, then we are done and things are simple. However, if the side is adjacent to an interior node, then we must traverse down the interior node to find the correct adjacent leaf node. This is where the quad tree information comes in. Remember that the adjacent oct tree nodes form a quad tree when projected onto the crossing side.

The algorithm for traversing the quad tree is straightforward and uses very similar techniques to the algorithm above. Its derivation is left as an exercise to the reader.

Since the algorithm goes directly from one leaf node to the next, each leaf node must contain information about its location in the tree in order to compute the appropriate corner value. This is why the position information is stored in the leaf node data structure above.

The final algorithm looks like the following:

leaf_node_cur = leaf_node_find_from_point(point_start);

// pre-compute the x, y, z deltas from the ray origin to the end point
oe_delta_x = point_end_x - point_start_x;
oe_delta_y = point_end_y - point_start_y;
oe_delta_z = point_end_z - point_start_z;

while(1)
{
    // do some processing on leaf_node_cur here

    // we need to move into the correct adjacent leaf node

    // First step is to determine which side of the octant we are leaving

    // do the xy plane test
    temp1 = oe_delta_y * (corner_x - point_start_x);
    temp2 = oe_delta_x * (corner_y - point_start_y);

    if(abs(temp1) > abs(temp2))
    {
        // the y axis is being crossed - the x axis is eliminated

        // now project onto the YZ plane
        temp1 = oe_delta_z * (corner_y - point_start_y);
        temp2 = oe_delta_y * (corner_z - point_start_z);

        if(abs(temp1) > abs(temp2))
        {
            // we are crossing the z axis
        }
        else
        {
            // we are crossing the y axis
        }
    }
    else
    {
        // the x axis is being crossed - the y axis is eliminated

        // now project onto the XZ plane
        temp1 = oe_delta_z * (corner_x - point_start_x);
        temp2 = oe_delta_x * (corner_z - point_start_z);

        if(abs(temp1) > abs(temp2))
        {
            // we are crossing the z axis
        }
        else
        {
            // we are crossing the x axis
        }
    }

    // look up the adjacent node info
    node_adjacent = node_adjacent_lookup(leaf_node_cur, side_crossing_index);
 
    if(node_is_outside_environment(node_adjacent)) break;

    if(node_is_pointing_to_quad_tree(node_adjacent))
    {
        // traverse down quad tree until the correct leaf node is found
    }

    leaf_node_cur = node_adjacent;
}

This means that to transition from one leaf node to the next costs 4 subtractions, 4 multiplies, 2 absolute values, and 2 compares. Note that this does not include the additional work to traverse down the quad tree if that is needed. The actual speed of the algorithm is determined by how many nodes are visited along the ray and by the memory bandwidth used to read the octant data structures. This is one of the reasons for the compact data structure presented above.

Using Ray Casting for Hidden Surface Complexity Reduction

The basic idea behind the algorithm for hidden surface complexity reduction is to cast many rays from the camera location to all areas of the view frustum. A ray is terminated when it leaves the environment or it collides with a primitive in the environment. When a ray passes through a leaf octant, all the primitives of that octant are drawn. Therefore, as the rays are traversed across the view frustum, the visible octants are found and their primitives are displayed.

Care must be taken not to cast too many rays, as the number of rays cast directly impacts the frame rate. Several optimizations can be made regarding how many rays are used in a single frame and the pattern of the rays.

Temporal locality can be taken advantage of by changing the location of the rays over time. A temporal pattern can be used which repeats every n frames, where n is some small number. The visibility algorithm then needs to be changed slightly so that a primitive is drawn only if it has been touched within the past n frames. This does have the disadvantage of potentially creating some popping of primitives at the edges of the view frustum when the visible set is changing quickly. An example of this situation is when the camera is following a fast moving character.

Grouping rays close together can leverage spatial locality. This way the octant data structures stay in cache for subsequent ray casts. Traversing the view frustum like a quad tree creates an efficient two-dimensional pattern.

Both of these techniques are used in Oni.

Using Ray Casting for Line Collision Detection

Often in a game it is useful to know if a ray intersects with some primitive in the environment. For example, this could be used to detect when a bullet or laser sight hits a wall. This process is a direct application of the ray cast algorithm but simply returns more information, such as which primitive was hit and its point of intersection.

Sphere Collision Detection

Sphere collision is another important test in a game. For example, sphere collision is needed to detect if a character has collided with the environment. In this case a sphere containing the character needs to be projected along a ray to see if any collisions occur. A ray is used instead of a point to prevent a fast moving character or object from missing a collision due to the possibility that in the last frame it was in front of the primitive and in the current frame it moved completely past the primitive.

This algorithm does not use a ray cast but does rely on the oct tree data structure. The idea is to first find the leaf octant that contains the ray start point and then recursively visit all adjacent nodes that intersect the Òhot dogÓ shaped geometry formed by the sphere projected along the ray. All of the primitives contained within the intersecting leaf octant nodes are then checked as well. Any that intersect the hotdog are reported as a collision.

The key for this algorithm to be efficient is a fast test to check if the octant intersects the hot dog. To date the author has not seen such a test. However, there does exist a very fast test for cube-sphere intersection [2]. In order to take advantage of this test we must iterate over the hotdog in several steps using a sphere to approximate the hotdog shape.

In Oni it is not that often that the length of the ray is significantly greater than the radius of the sphere. In other words, collision tends to happen on fat spheres over short distances. In these cases it is not necessary to iterate over the ray. It was also found that faster moving projectiles such as bullets and lasers did not require sphere collision, therefore line collision was used instead.

Note that if only a single primitive is needed as a collision result, then using the line collision test first can be a good trivial acceptance case. The results of the sphere collision test can be fed into a more detailed, but more expensive collision check routine, such as a bounding box test.

Problems

The primary issue with this approach to hidden surface complexity reduction is that on the current generation of machines not enough rays can be cast to cover the entire view frustum adequately. This can result in ray casting missing octants far from the camera location. When an octant is missed, its primitives are not drawn, which results in holes appearing in the environment. Even worse, some primitives in the distance can flash in and out.

There are some ways to minimize this issue. The obvious is to simply cast more rays but this can result in loss of frame rate. Another approach is to limit how far into the distance the environment can be seen with fogging or authoring constraints. Lastly, the algorithm could be modified to include some heuristics to find octants that should be visible but are not. For example, if an octant that is not visible straddles two visible octants, then make it visible anyway. This can be thought of as applying a low-pass filter to smooth out the high frequency noise.

Areas for Future Development

This algorithm has a lot of potential for the next generation of machines with faster processors and memory subsystems. It could be used to provide ray trace-like information for rendering. For example, rays could be cast from a moving light source to light map pixels on the environment so that the light can cast real-time shadows. This technique would allow moving lights sources to cast shadows. With the addition of placing dynamic objects in the oct tree data structure this could be used to allow moving lights to cast shadows from moving objects.

While the author is not an expert at hardware design in any sense, given the simple nature of the algorithm it does seem possible that this algorithm could be implemented in hardware and used as part of a hardware ray tracing solution. In essence this would be the combination of an algorithm already implemented in hardware, the Bresenham algorithm, and an intelligent DMA engine that can follow pointers [3][4].

The algorithm could also be extended to account for large dynamic object that can occlude visibility by incorporating them into the oct tree data structure and allowing the visibility ray casting to collide against them.

Conclusion

This algorithm is not designed to be faster than traditional approaches using BSP trees. It is designed to allow more freedom to the environment creators. During the environment creation process there is no need for portals. In particular, Oni has many environments where a portal system could potentially be problematic. These environments include large atrium spaces where the player can see into the building across the street and long hallways with glass that run down its entire length.

Due to the problems with this algorithm its use is not for everyone. For games where large realistic indoor-outdoor spaces that are designed by more traditional architects are required this algorithm can work quite well. For games that take place primarily indoors or in simpler environments a traditional BSP tree approach is more suitable.

Acknowledgements

I would like to thank Quinn Dunki, Michael Evans, and Kevin Armstrong for their contributions and suggestions as members of the Oni engineering team. Sun-Inn Shih, Jeff White, Andrew Kirmse, and Chris Hecker gave thoughtful reviews. Finally, I would like to thank Alex Seropian of Bungie Software for supporting the Oni project and giving permission to publish this paper.

Appendix A

typedef unsigned short ty_uns16;
typedef unsigned long ty_uns32;

// This enumerates the 6 possible sides of a cube that defines an octant
enum ty_octant_side
{
     nc_octant_side_x_pos,
     nc_octant_side_x_neg,
     nc_octant_side_y_pos,
     nc_octant_side_y_neg,
     nc_octant_side_z_pos,
     nc_octant_side_z_neg,
 
     nc_octant_side_num
};

// This enumerates the 3 bit positions for the x, y, and z axes
enum ty_octant_axis_bit
{
     nc_octant_axis_x_bitpos,
     nc_octant_axis_y_bitpos,
     nc_octant_axis_z_bitpos
};

// This enumerates the 8 combinations of dividing an octant to form its children
enum ty_octant_children
{
     nc_octant_child_nz_ny_nx,
     nc_octant_child_nz_ny_px,
     nc_octant_child_nz_py_nx,
     nc_octant_child_nz_py_px,
     nc_octant_child_pz_ny_nx,
     nc_octant_child_pz_ny_px,
     nc_octant_child_pz_py_nx,
     nc_octant_child_pz_py_px,
 
     nc_octant_child_num
 
};

// This is an octant interior node that simply points to its 8 children
typedef struct ty_octant_node_interior
{
     ty_uns16 children[nc_octant_child_num]; // If the high bit is set then it points into the
octant leaf node list.
                      // Otherwise it points into the octant interior node list
} ty_octant_node_interior;

// This is an octant leaf node. It contains references to all primitives
// that intersect it, its dimension and position information, and its
// adjacency  information
typedef struct ty_octant_node_leaf
{
     ty_uns32 primitive_indirect_index_encode; // This is stored as a 24 bit offset and a 8 bit
length.
           // The offset points into primitive_index_array(below)
           // and the length is how many indices are in the octant
 
     ty_uns32 dimension_encode; // This encodes the size of the octant and its position
              // in the tree. It is encoded as follows:
              // 5 bits - leaf node size
              // 9 bits - max x position
              // 9 bits - max y position
              // 9 bits - max z position
 
     ty_uns16 adjacency_indices[nc_octant_side_num]; // If the high bit is set then it points to
the octant leaf node.
           // Otherwise it points into the quad tree list
 
} ty_octant_node_leaf;

// This enumerates the 4 possible children of a quad tree interior node
enum
{
     nc_quadrant_side_u_pos,
     nc_quadrant_side_u_neg,
     nc_quadrant_side_v_pos,
     nc_quadrant_side_v_neg,
 
     nc_quadrant_side_num
};

// This is a quad tree interior node that simply points to its 4 children or to oct tree leaf nodes
typedef struct ty_quadrant_interior_node
{
     ty_uns16 children[nc_quadrant_side_num]; // If high bit it set then it points into octant leaf
node.
           // Otherwise it points into a quad tree interior node
 
} ty_quadrant_interior_node;

// This is the main oct tree data structure
typedef struct ty_oct_tree
{
     // The list of oct tree interior nodes. The root is at octant_node_interior_array[0]
     ty_uns16      octant_node_interior_num; // The number of nodes
     ty_octant_node_interior* octant_node_interior_array; // The array of nodes
 
     // The list of oct tree leaf nodes.
     ty_uns16     octant_node_leaf_num; // The number of nodes
     ty_octant_node_leaf* octant_node_leaf_array; // The array of nodes
 
     // The list of quad tree interior nodes. There are no leaf nodes because the quad tree interior
     // node will point directly to the oct tree leaf node.
     ty_uns16      quadrant_node_interior_num; // The number of nodes
     ty_quadrant_interior_node* quadrant_node_interior_array; // The array of nodes
 
     // The list of primitive indices
     ty_uns32   primitive_index_num; // The number of indices
     ty_uns16*   primitive_index_array; // The indices
 
} ty_oct_tree;

References:

[1] "Graphics Programming Black Book," Michael Abrash, 1997.
[2] "Graphics Gems I," Andrew S. Glassner, 1995, pages 335-339.
[3] "Hardware Accelerated Rendering of CSG and Transparency" M. Kelley, K. Gould, B. Pease, S. Winner, A. Yen SIGGRAPH 1994
[4] "Hardware Accelerated Rendering of Antialiasing Using a Modified A-Buffer Algorithm" B. Rivard, S. Winner, M. Kelley, B. Pease, A. Yen SIGGRAPH 1997